どうもリンです。
最近はデータ数が少ない状況での機械学習案件が多く、決定木系アルゴリズムが大活躍です。
アルゴリズムの原理や得意不得意はかなり理解している方だと思いますが、挙動についての知見はまだまだ浅いのです。。
そこで今日は決定木系アルゴリズムの挙動を観察しましょう。
- 決定木
- ランダムフォレスト
- LightGBM
これら決定木系アルゴリズムがどのような予測挙動を見せるのかを分析して少し知見を広げてみましょうってお話です。
モチベーション:決定木系アルゴリズムの比較
今回のモチベーションは「決定木系アルゴリズムの予測線はどうなっているか」です。
決定木系ですから説明変数軸に平行or垂直な予測線しか引けないことは広く知られています。
- 決定木の予測線はどうなる?
- ランダムフォレストの予測線はどうなる?
この辺りは原理を知っている方なら想像に難くないかと思います。
しかし、面倒くさくて実物の予測線を見たことはないのではないかと思います。(私もです)
- LightGBMの予測線はどうなる?
この辺りはもはや想像できない方も多いのではないでしょうか?
今回はそんな予測線を実際に引いてみて知見を深めてみましょう。
原理についておさらい

決定木系アルゴリズムの原理も知らないや。
って方も沢山いると思いますので、原理についての記事を貼っておきます。
ここらの記事を読めば大体の原理は理解できるでしょう。
より詳細な原理が知りたい方は論文もしくは私の書籍をご覧ください。
「説明変数の相互作用を反映する」とは?
決定木系アルゴリズムは分岐を繰り返すことで「説明変数同士の相互作用を反映する」と言われています。
まぁよく考えればそうですよね。
しかし、直接観察してみないと科学者(機械学習エンジニア)としてダメだと勝手に思いました。
今回はそんなモチベーションで頑張ってみましょう!
単項式の回帰問題
まずは単項式から行きましょう。
※見苦しいコードが続きますが、基本文章と図だけ見ていただければ理解できます。コードは読み飛ばしながらお進みください。
データセット準備
ライブラリのインポート
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 | import pandas as pd import numpy as np #データ可視化ライブラリ import matplotlib.pyplot as plt from matplotlib import cm import seaborn as sns #決定木ライブラリ from sklearn import tree #ランダムフォレストライブラリ from sklearn.ensemble import RandomForestRegressor #LightGBMライブラリ import lightgbm as lgb #訓練データとモデル評価用データに分けるライブラリ from sklearn.model_selection import train_test_split #ノイズを出力するランダムライブラリ import random #3Dグラフ描写ライブラリ from mpl_toolkits.mplot3d import Axes3D #R2値計算用 from sklearn.metrics import r2_score |
今回の一次関数を用意します。
1 2 3 | x = np.arange(-15, 15, 0.05) y = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) + random.uniform(-0.001,0.001) for x in x] y_true = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) for x in x] |
正規分布様の関数を用意しました。
xは-15~15を0.05刻みで生成します。yはxを関数に入れてノイズを加えます。
y_trueはノイズが入っていない値です。
今回はxとyを使ってモデルを訓練していきます。上手くノイズを避けることができるかな?
データフレームを用意しておきましょう。
1 2 | df = pd.DataFrame([x, y]).T df.columns=['x', 'y'] |

↑dfの中身はこんな感じ
可視化しましょう。y_trueも添えて。
1 2 3 | plt.scatter(df['x'], df['y']) plt.plot(df['x'], y_true, marker=None, linewidth=4, color="black") plt.ylim(-0.0025, 0.0125) |
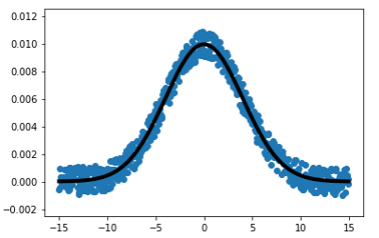

青点がノイズあり。黒線がノイズなしです。
ここから青点を機械学習にぶち込みます。
そして非常に細かく刻んだxの値を与えて予測値を出します。
その予測値を可視化すれば機械学習の予測線が見えるはずですね!
決定木
では手始めに決定木からいきましょうか。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #決定木を学習 clf = tree.DecisionTreeRegressor(max_depth=100) model = clf.fit(df.drop('y', axis=1), df['y']) #予測させるxの配列を作る。(非常に細かく刻んだ) x_test = np.arange(-15, 15, 0.01) #y_true(ノイズなし)をx_testで新しく作っておく。 y_true = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) for x in x_test] #決定木で予測させる predicted = np.array([model.predict(np.array([x_test]).T)]) #予測値をx座標と結合させる pred_df = pd.DataFrame([x_test, predicted.T]).T pred_df.columns=['x', 'y'] #可視化する plt.plot(x_test, y_true, marker=None, linewidth=4, color="black") plt.scatter(df['x'], df['y'], s=5) plt.plot(pred_df['x'], pred_df['y'], linewidth=2, color="red", alpha=0.7) plt.ylim(-0.0025, 0.0125) plt.show() #予測精度を出力する print(r2_score(y_true, pred_df['y'])) |
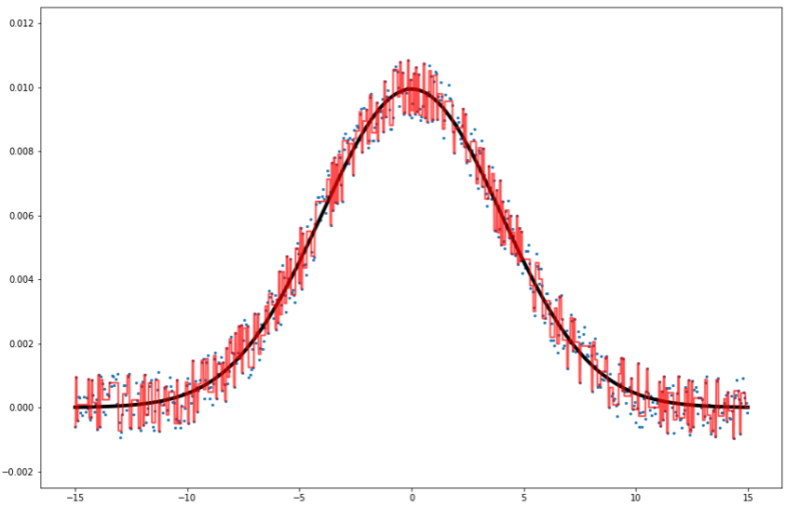

R^2値は0.975でした。
青点がノイズありの値でしたね。こいつを機械学習に入れて学習させました。
予測させたかった値は黒線です。ノイズなしってやつね。
そして赤線が決定木の予測線です。非常に細かいxの値を決定木に入れることで予測線を可視化できました。
かなり過学習していますね?
ノイズを無視できなかったようです。
少し拡大しましょう。
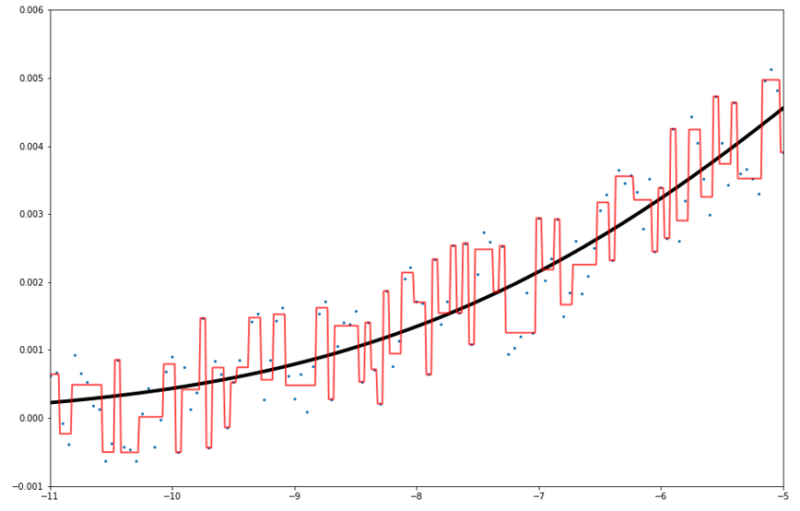

学習させた青点に引っ張られています。
「決定木の予測線は説明変数と並行or垂直になる」とはこのグラフを見ると明らかですよね。
分岐を繰り返す中で、「-8.8<x<-9.2ならばy=0.0004」というように予測線を作っていきます。
これがそのまま予測線として可視化されていますね。
ランダムフォレスト
では続いてランダムフォレストです。決定木と同じようなコードを書きましょう。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #ランダムフォレストを学習 clf = RandomForestRegressor(n_estimators=100) model = clf.fit(df.drop('y', axis=1), df['y']) #予測させるxの配列を作る。(非常に細かく刻んだ) x_test = np.arange(-15, 15, 0.01) #y_true(ノイズなし)をx_testで新しく作っておく。 y_true = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) for x in x_test] #ランダムフォレストで予測させる predicted = np.array([model.predict(np.array([x_test]).T)]) #予測値をx座標と結合させる pred_df = pd.DataFrame([x_test, predicted.T]).T pred_df.columns=['x', 'y'] #可視化する plt.plot(x_test, y_true, marker=None, linewidth=4, color="black") plt.scatter(df['x'], df['y'], s=5) plt.plot(pred_df['x'], pred_df['y'], linewidth=2, color="red", alpha=0.7) plt.ylim(-0.0025, 0.0125) plt.show() #予測精度を出力する print(r2_score(y_true, pred_df['y'])) |
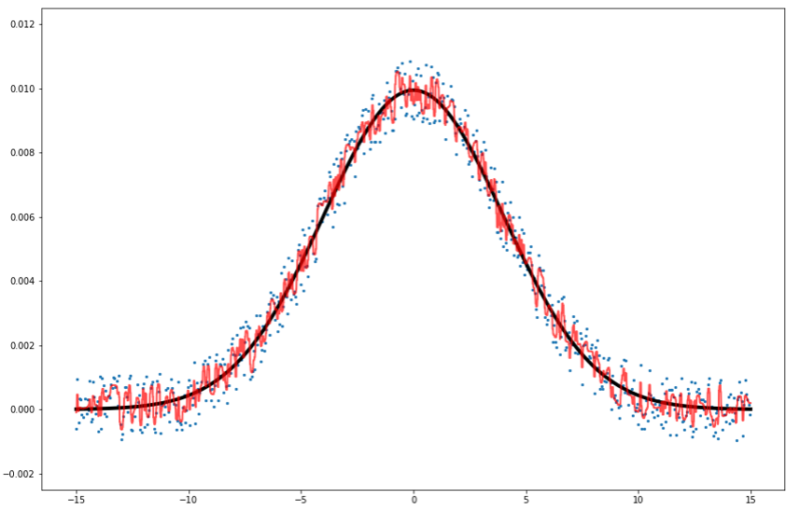

R^2値は0.989でした。決定木は0.975だったので少し改善。
拡大してみましょう。
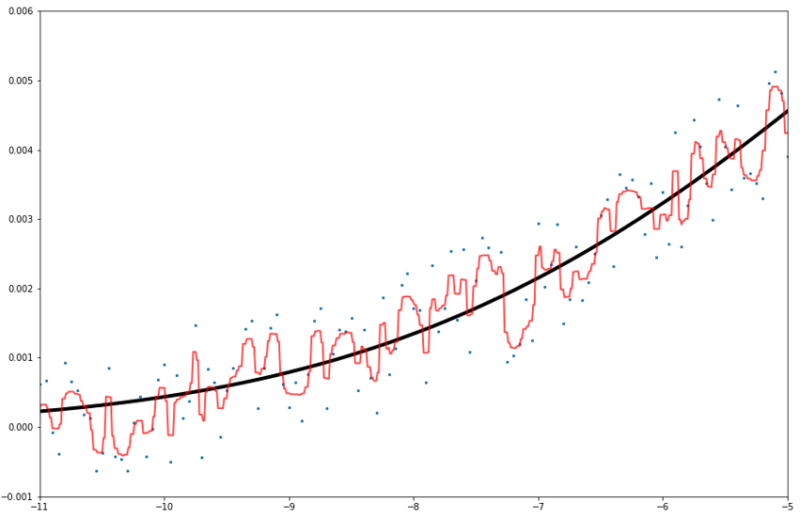

なるほどなるほど。予測線のカクカクがかなり細かくなっていますね。
これはランダムフォレストが「様々な決定木の寄せ集め」であるからですね。
しかし過学習は相変わらず生じています。決定木よりはマシになりましたがね。
LightGBM
ではLightGBMです。LightGBMはハイパーパラメータチューニングをしなければいけないのですが、面倒なのでOptunaのステップワイズ法に頼りましょう。
↓詳しくはこちら。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 | #ハイパーパラメータチューニングの参照用に訓練データとテストデータに分割する train_set, test_set = train_test_split(df, test_size=0.2, random_state=4) #訓練データを説明変数データ(X_train)と目的変数データ(y_train)に分割 X_train = train_set.drop('y', axis=1) y_train = train_set['y'] #モデル評価用データを説明変数データ(X_train)と目的変数データ(y_train)に分割 X_test = test_set.drop('y', axis=1) y_test = test_set['y'] #ハイパーパラメータチューニング自動化ライブラリ import optuna #LightGBM用Stepwise Tuningに必要 from optuna.integration import lightgbm_tuner #LightGBM用データセットに変換 lgb_train = lgb.Dataset(X_train, y_train) lgb_eval = lgb.Dataset(X_test, y_test) #最小限のパラメータ設定 params = {'objective': 'regression', 'metric': 'rmse'} #Optuneの最適化パラメータ保存用 best_params = {} #Optunaのステップワイズパラメータチューニング gbm = lightgbm_tuner.train(params, lgb_train, valid_sets=lgb_eval, num_boost_round=10000, early_stopping_rounds=100, verbose_eval=50, best_params=best_params) |
まずはOptunaのハイパーパラメータチューニングをさせて、最適なパラメータを探します。
計算が終わったらbest_paramsに格納してくれます。とってもべんり。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | #青点(予測させる点)をLightGBM用データセットに変換 lgb_alldata = lgb.Dataset(df.drop('y', axis=1), df['y']) #best_paramsを使ってLightGBMを学習させる gbm = lgb.train(best_params, lgb_alldata, num_boost_round=700, early_stopping_rounds=None, verbose_eval=50) x_test = np.arange(-15, 15, 0.01) y_true = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) for x in x_test] predicted = np.array([gbm.predict(np.array([x_test]).T)]) pred_df = pd.DataFrame([x_test, predicted.T]).T pred_df.columns=['x', 'y'] plt.figure(figsize=(15,10)) plt.plot(x_test, y_true, marker=None, linewidth=4, color="black") plt.scatter(df['x'], df['y'], s=5) plt.plot(pred_df['x'], pred_df['y'], linewidth=2, color="red", alpha=0.7) plt.ylim(-0.0025, 0.0125) plt.show() print(r2_score(y_true, pred_df['y'])) |
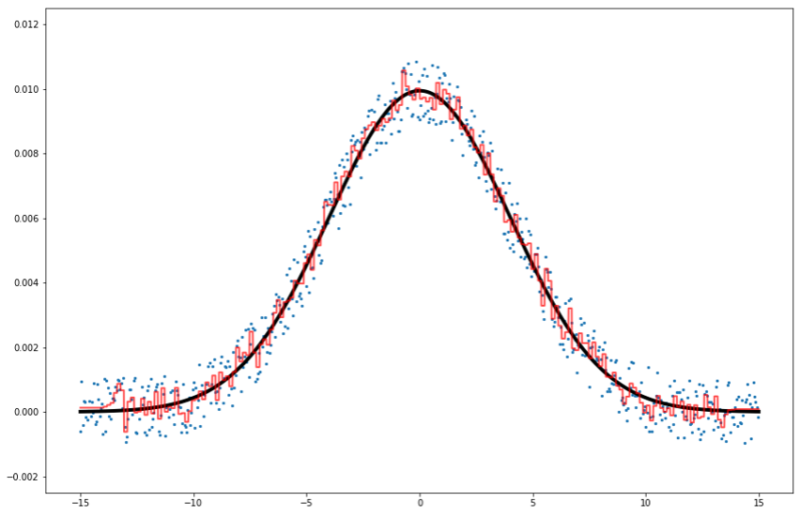

R^2値は0.991でした。ランダムフォレストが0.989、決定木は0.975だったのでまた少し改善。
拡大します。
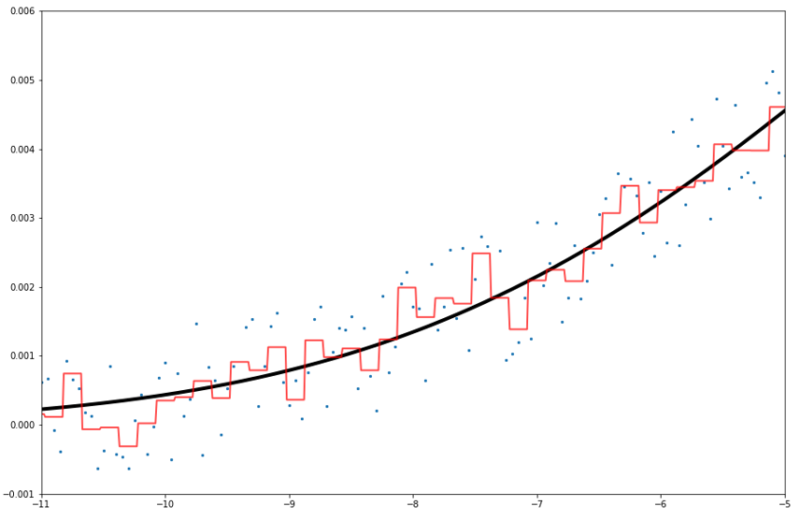

まあ少し過学習していますが、良い感じではないでしょうか?決定木よりは確実に過学習は減少傾向です。
予測線は意外にもカクカクしていますね。ランダムフォレストのように平滑線にならないようです。
おまけ:重回帰分析
こんな非線形関係のデータに、線形回帰の重回帰分析で学習するとどうなるでしょうか?
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | from sklearn import linear_model clf = linear_model.LinearRegression() model = clf.fit(df.drop('y', axis=1), df['y']) x_test = np.arange(-15, 15, 0.01) y_true = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) for x in x_test] predicted = np.array([model.predict(np.array([x_test]).T)]) pred_df = pd.DataFrame([x_test, predicted.T]).T pred_df.columns=['x', 'y'] plt.figure(figsize=(15,10)) plt.plot(x_test, y_true, marker=None, linewidth=4, color="black") plt.scatter(df['x'], df['y'], s=5) plt.plot(pred_df['x'], pred_df['y'], linewidth=2, color="red", alpha=0.7) #plt.xlim(-11,-5) #plt.ylim(-0.001,0.006) plt.ylim(-0.0025, 0.0125) print(r2_score(y_true, pred_df['y'])) |
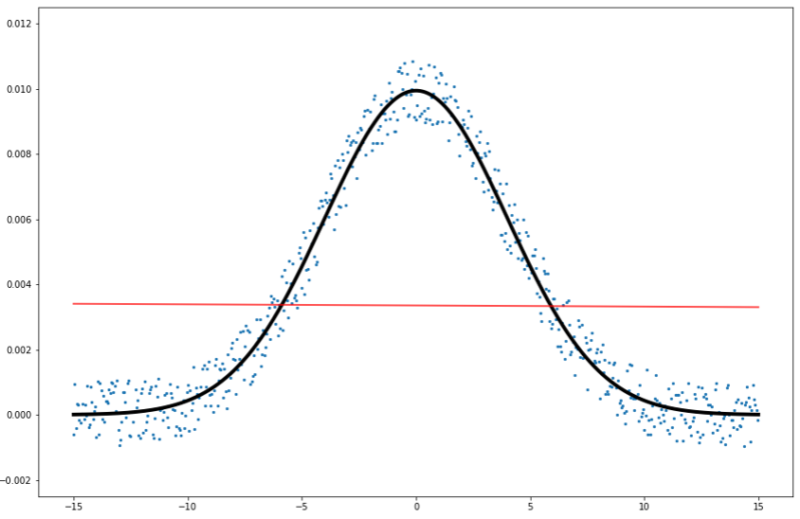

重回帰分析は説明変数と目的変数が線形関係にあることが前提なので、今回のような非線形関係では機能しません。
データ数が少ないと?
「LightGBMのようなブースティング系はデータ数が少ないと機能しない」と言われますが、確認してみましょうか。
1 2 3 | x = np.arange(-15, 15, 1) y = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) + random.uniform(-0.001,0.001) for x in x] y_true = [np.exp(-(x**2)/(2*sigma**2)) / (2*np.pi*sigma**2) for x in x] |
学習させるデータを作るコードでしたね。
x = np.arange(-15, 15, 0.05)→x = np.arange(-15, 15, 1)に変更しました。
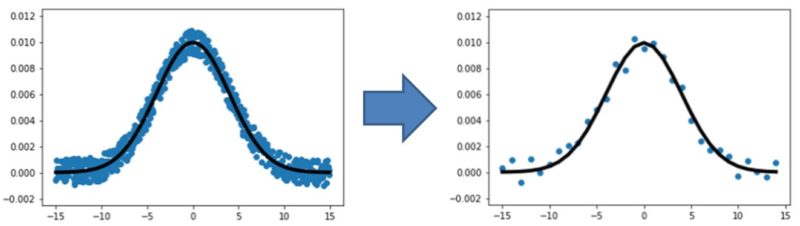

学習で使えるデータ数はこんなにも少なくなっちゃいました。
では決定木・ランダムフォレスト・LightGBMの予測線はどう変わるでしょうか?
結果だけ書きます。(LightGBMはハイパーパラメータチューニングし直しました)
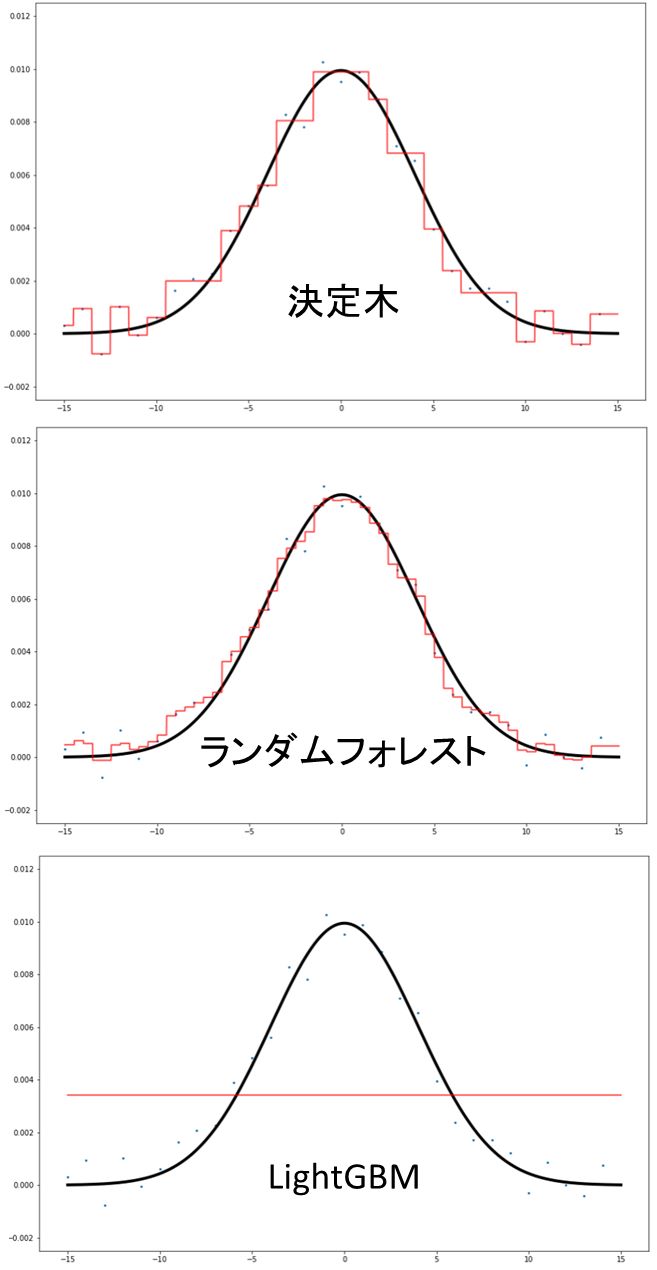

LightGBMの予測線が平坦になってしまいましたね。
やはりデータ数が少ないとき、ブースティング系は機能しないようです。
二項式の回帰問題
単項式の回帰線は見たことあったのですが、二項式の予測線となるとどのサイトでも見たことはないですね。
ということで見ていきましょうか!
データセット準備
まずはデータセットの準備から。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | x = y = np.arange(-15, 15, 0.5) X, Y = np.meshgrid(x, y) sigma = 4 Z = np.exp(-(X**2 + Y**2)/(2*sigma**2)) / (2*np.pi*sigma**2) fig = plt.figure(figsize=(10,10)) ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm) ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("f(x, y)") plt.show() |
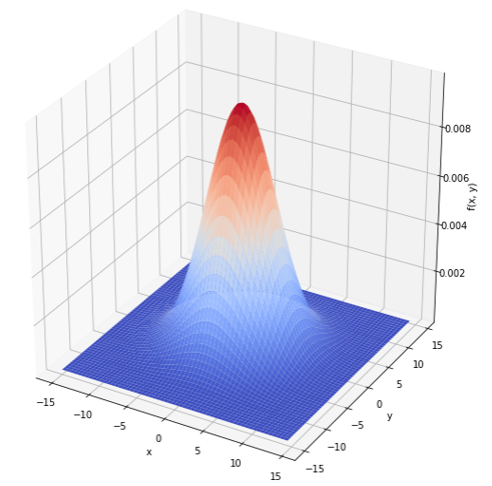

こんな感じの多項式正規分布様のプロットを機械学習に学習させましょう!今回はノイズなしで!
プロットの密度はこんな感じです。
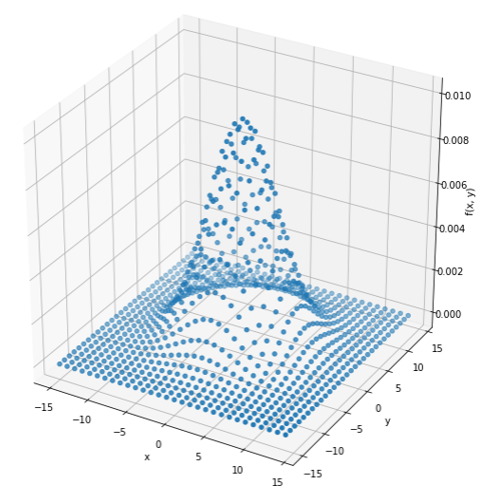

まあまあな密度ですね。きちんと予測できるでしょうか?
予測線の出力は、↑よりも密度の濃いプロット(xとyの値)を与えることで可視化します。
↑のプロットの間はどのような予測線になっているのかを見てみましょう。
1 2 3 4 5 6 7 | x = X.ravel() y = Y.ravel() z = Z.ravel() df = pd.DataFrame([x,y,z]).T df.columns=['x', 'y', 'z'] |
↑x,y,zを機械学習モデルが読み込めるような形に加工します。
さっきの3D可視化はメッシュグリッドというnumpy処理をさせていたので、機械学習モデルに入れるように加工しなければいけないのです…
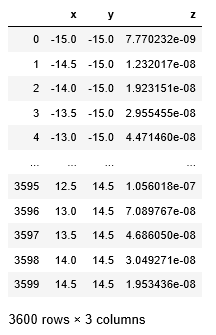

↑dfはこんな感じ。全座標のx,y,z座標が載っています。
このdfを決定木・ランダムフォレスト・LightGBMに学習させます。
そしてもっと細かなプロットを予測させ、予測線を可視化しましょう。
決定木
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #決定木で学習させる clf = tree.DecisionTreeRegressor(max_depth=100) model = clf.fit(df.drop('z', axis=1), df['z']) #予測線用のx,yプロットを作る x_test = y_test = np.arange(-15, 15, 0.1) X_test, Y_test = np.meshgrid(x_test, y_test) #決定木に予測させる&3D可視化用の形に加工する arr = np.empty((0,len(X_test)), int) for i in range(len(Y_test)): predicted = np.array([model.predict(np.array([X_test[i],Y_test[i]]).T)]) arr = np.append(arr, predicted, axis=0) #3D可視化する fig = plt.figure(figsize=(10,10)) ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X_test, Y_test, arr, rstride=1, cstride=1, cmap=cm.coolwarm) ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("f(x, y)") plt.show() |
とっても分かりにくいコードでごめんなさい。
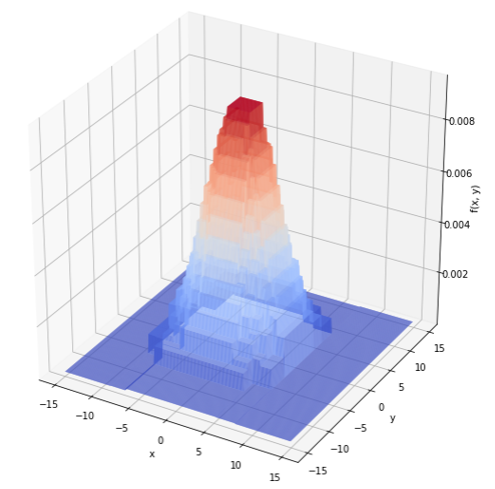

↑このような予測線が出力されました。
やはりカクカクですね。2項式なのでx軸y軸z軸に平行or垂直に予測線が走るようです。原理を考えればあたりまえですね。
ランダムフォレスト
つづいてランダムフォレストです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | #ランダムフォレストで学習させる clf = RandomForestRegressor(n_estimators=100) model = clf.fit(df.drop('z', axis=1), df['z']) #予測線用のx,yプロットを作る x_test = y_test = np.arange(-15, 15, 0.1) X_test, Y_test = np.meshgrid(x_test, y_test) #ランダムフォレストに予測させる&3D可視化用の形に加工する arr = np.empty((0,len(X_test)), int) for i in range(len(Y_test)): predicted = np.array([model.predict(np.array([X_test[i],Y_test[i]]).T)]) arr = np.append(arr, predicted, axis=0) #3D可視化する fig = plt.figure(figsize=(10,10)) ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X_test, Y_test, arr, rstride=1, cstride=1, cmap=cm.coolwarm) ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("f(x, y)") plt.show() |
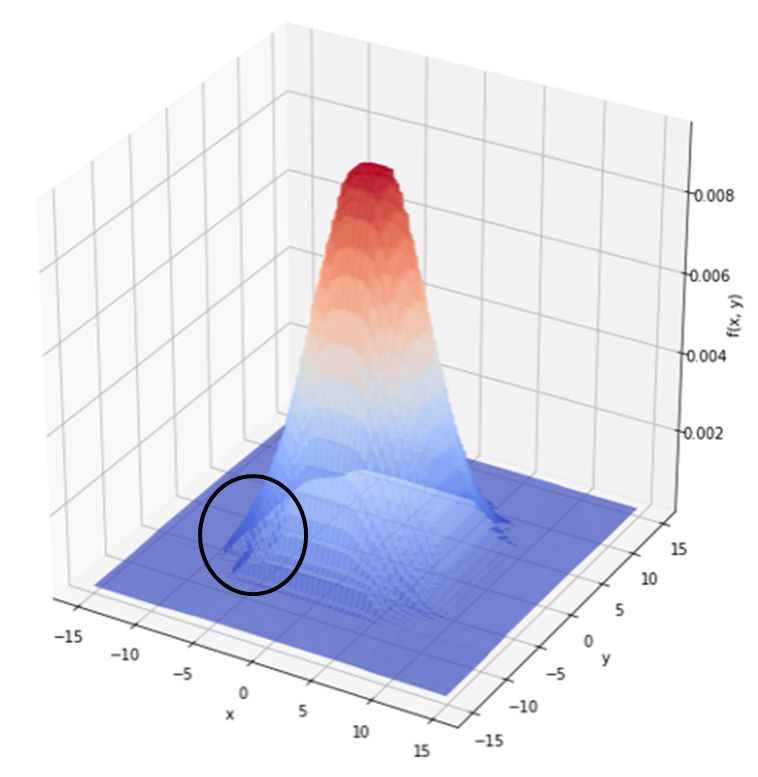

決定木より幾分か性能が上がりましたね。黒丸の部分を拡大してみます。


少しカクカクですね。本来ならば淵はまるーくなるはずなのですが。
けれど複数の決定木によりかなり実態に近くなっています!
LightGBM
そしてLightGBMです。
1 2 3 4 5 6 7 8 9 10 11 12 | train_set, test_set = train_test_split(df, test_size=0.2, random_state=4) #訓練データを説明変数データ(X_train)と目的変数データ(y_train)に分割 XY_train = train_set.drop('z', axis=1) z_train = train_set['z'] #モデル評価用データを説明変数データ(X_train)と目的変数データ(y_train)に分割 XY_test = test_set.drop('z', axis=1) z_test = test_set['z'] lgb_train = lgb.Dataset(XY_train, z_train) lgb_eval = lgb.Dataset(XY_test, z_test) |
まずはハイパーパラメータチューニング様に訓練データとテストデータに分割します。
1 2 3 4 5 6 7 8 9 10 11 12 | params = {'objective': 'regression', 'metric': 'rmse'} best_params = {} gbm = lightgbm_tuner.train(params, lgb_train, valid_sets=lgb_eval, num_boost_round=10000, early_stopping_rounds=100, verbose_eval=50, best_params=best_params) |
そしてoptunaのステップワイズ法でbest_paramsを出力させます。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 | lgb_alldata = lgb.Dataset(df.drop('z', axis=1), df['z']) gbm = lgb.train(best_params, lgb_alldata, num_boost_round=7500, early_stopping_rounds=None, verbose_eval=50) x_test = y_test = np.arange(-15, 15, 0.1) X_test, Y_test = np.meshgrid(x_test, y_test) arr = np.empty((0,len(X_test)), int) for i in range(len(Y_test)): predicted = np.array([gbm.predict(np.array([X_test[i],Y_test[i]]).T)]) arr = np.append(arr, predicted, axis=0) fig = plt.figure(figsize=(10,10)) ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X_test, Y_test, arr, rstride=1, cstride=1, cmap=cm.coolwarm) ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("f(x, y)") plt.show() |
ほんでbest_paramsを使ってLightGBMで学習&予測!
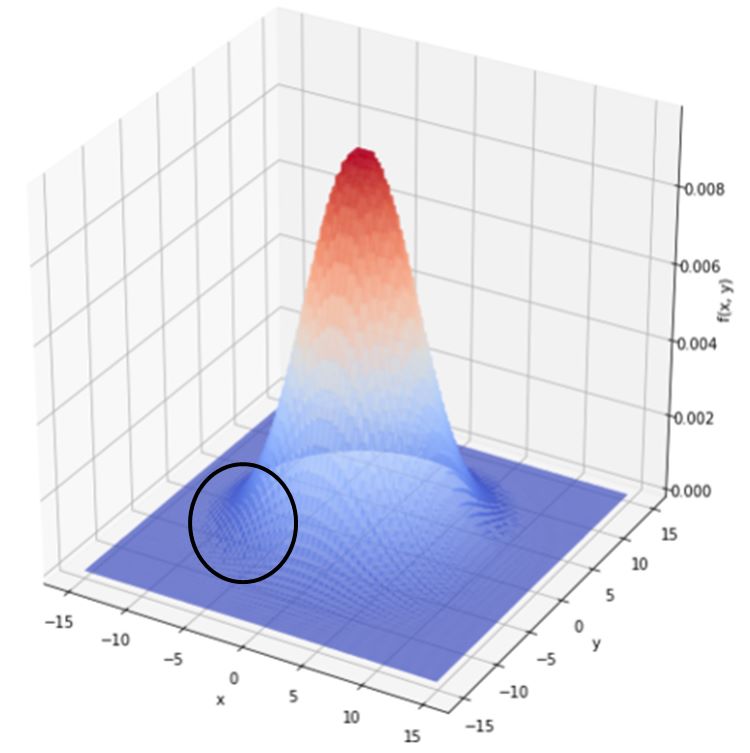

ほう!予測線がかなり平滑ですね!黒丸拡大します。


あーこれこれ。この平滑さが正しい姿ですよね。
よって2項式の場合もLightGBMが強いということでした。
ちなみに重回帰分析
おまけです。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | clf = linear_model.LinearRegression() model = clf.fit(df.drop('z', axis=1), df['z']) x_test = y_test = np.arange(-15, 15, 0.1) X_test, Y_test = np.meshgrid(x_test, y_test) arr = np.empty((0,len(X_test)), int) for i in range(len(Y_test)): predicted = np.array([model.predict(np.array([X_test[i],Y_test[i]]).T)]) arr = np.append(arr, predicted, axis=0) fig = plt.figure(figsize=(10,10)) ax = fig.add_subplot(111, projection='3d') ax.plot_surface(X_test, Y_test, arr, rstride=1, cstride=1, cmap=cm.coolwarm) ax.set_xlabel("x") ax.set_ylabel("y") ax.set_zlabel("f(x, y)") plt.show() |
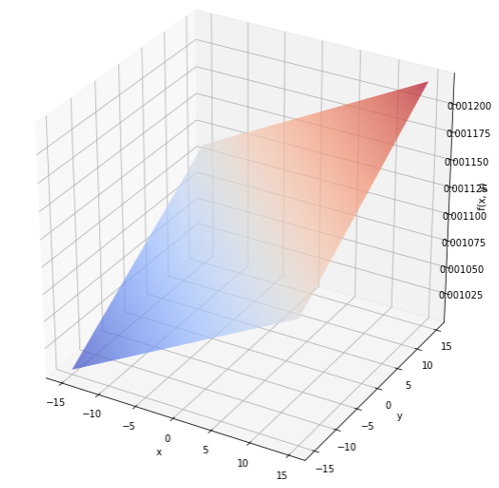

完全な出オチ。重回帰分析は説明変数と目的変数が線形でないときは効力を発揮しません。
考察
なぜLightGBMの精度が良いのか?
LightGBMは最初に決定木を構築した後に「誤差」を修正する決定木を次々に作るアルゴリズムでしたね。
一方でランダムフォレストは性格の異なる決定木の意見を統合するアルゴリズムでした。
私が思うに、ランダムフォレストは決定木の学習傾向から逸脱できないのだと思われます。
「直接目的変数を予測する決定木アルゴリズムとして学習しやすい方向性」が存在して、大多数の決定木がその方向に学習してしまう。これが学習誤差を生んでいるのでは?
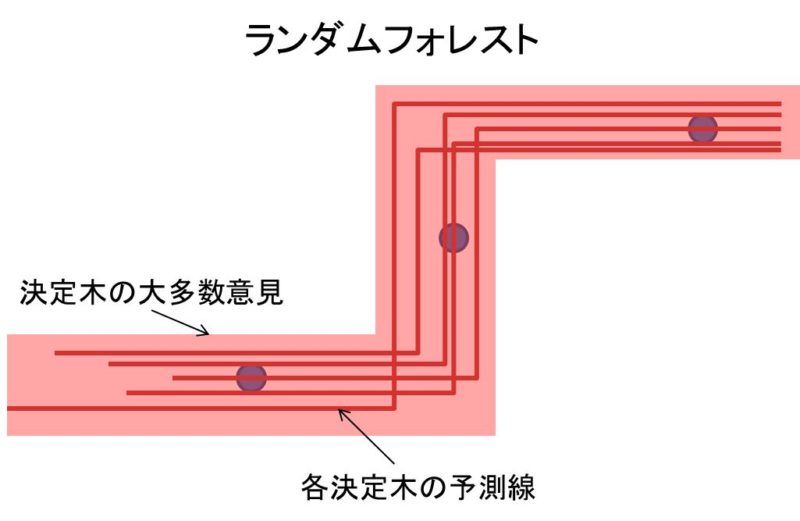

↑このような「大多数の決定木が通る領域」があり、
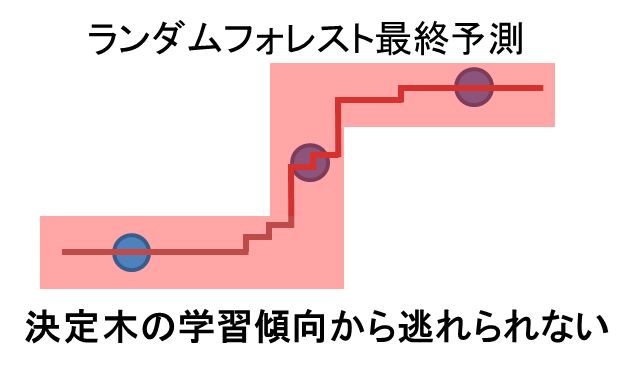

↑最終的な予測線もその領域から逃れられない。
青点を直線結んだ線が正解ですからどうしても誤差が大きくなります。
一方でLightGBMは1本の決定木から誤差修正を行っていきます。
2本目以降の決定木は誤差を予測するので、直接目的変数を予測するわけではありません。
よって決定木の学習傾向から逸脱した予測線が引けるのではないかと考えられます。
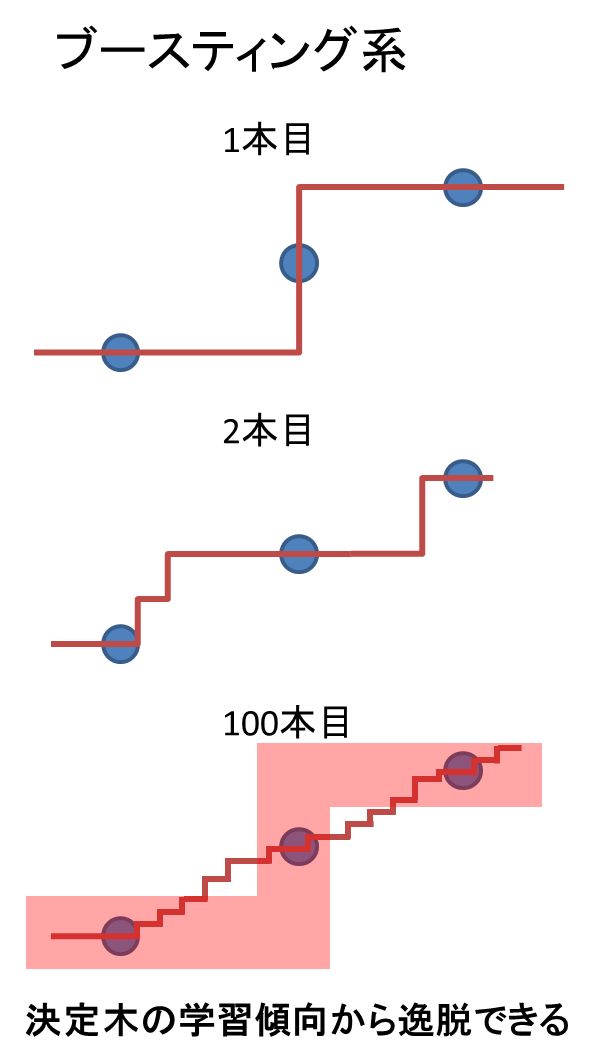

ただし誤差予測には相当数のデータ量が必要なようで、半端なデータ量ならばランダムフォレストのほうが効果的に予測線を多様化できるようですね。
単純な考察ですので、間違っているかもしれません。教えて強い人。
まとめ
ということで今回は決定木・ランダムフォレスト・LightGBMの予測線を可視化してみました。
モデル挙動について知見は深まったでしょうか?
本当に機械学習は奥が深いですよね。これからも色々な知見をお届けします。
違うアプローチでの挙動観察は私の教材からどうぞ!(宣伝)↓
機械学習完全マスター教科書販売中です(980円[期間限定]:24350文字の教科書です)
pythonの一般的な教本と一味違い、
- 第一に機械学習を最短経路で「実装」できる
- 第二に詳しい原理が理解できる
これらを重視して執筆しました。
普通の教本の1/4くらいの値段ですし、誰かに紹介すれば半額の紹介料が入るのですぐ元は取れます
★★★★★この価格でこのクオリティは凄すぎる
大学生ですが、これをつかって実験のレポートのデータ解析などにもつかえそうだと思いました! また、値段が安すぎて恐縮してます汗 凄すぎる…
レビュー欄より
★★★★★ 数ある教材の中でもトップクラスの分かりやすさ
これを機会に一度挫折したpythonを学び直そうと一念発起いたしました。いろいろなお勧めサイトの教材を拝見し購入しては失敗していましたが、ようやく超優良教材見つけました。知りたかった情報がすべて網羅されていて、この価格はなかなか無いと思います。今後の追加情報も期待したいです。
レビュー欄より
↑こんなコメントも頂きました!ありがとうございます(泣)
お役に立てて、必死に執筆した甲斐がありました(泣)(泣)
レビューはモチベに繋がるので、順次追記してコンテンツを増加していきます!乞うご期待!
追記[2020/03/14]:コンテンツ追加しました。
- ランダムフォレスト&LightGBM内部計算の可視化方法
- 内部可視化を基にした原理解説
- 学習の進行による予測分布の変化
- マテリアルズインフォマティクスへの活用方法
Python初心者であれば更に理解が深まり、玄人でも更なる原理や挙動の知見を得ることができるようになりました!
是非一読あれ~
↓リンク
機械学習はこれ一本!pythonインストール~機械学習実装まで完全理解講座
次の記事↓
↓ 効率的なPython学習はオンラインスクールがオススメ ↓






コメント